) que cumplen
sobre una imagen A las siguientes propiedades:
Los filtros morfológicos son operadores morfológicos
() que cumplen
sobre una imagen A las siguientes propiedades:
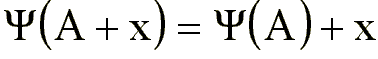
La erosión, dilatación,
opening y closing son invariantes ante una traslación, tanto para
el conjunto como para el elemento estructurante.
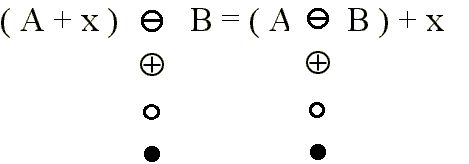
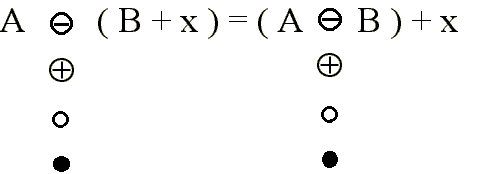
· Son monótonamente crecientes.
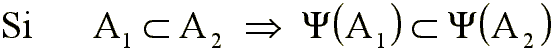
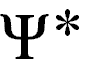es dual de
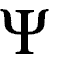si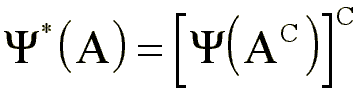 
La erosión es dual
de la dilatación.
.
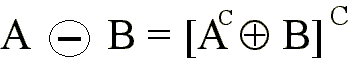
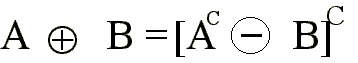
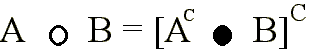
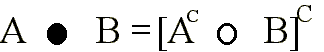
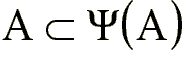Un filtro es antiextensivo si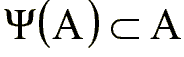 
.
El opening es antiextensivo: 
.
El closing es extensivo: 
.
La erosión es antiextensiva si el elemento estructurante contiene al origen, y la dilatación es extensiva si el elemento estructurante contiene al origen.
· Idempotencia.
Un filtro es idempotente si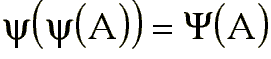 
.
El opening y el closing son idempotentes, es decir:
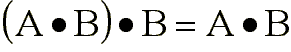
Filtrados óptimos.
El opening y el closing son, bajo algunas condiciones,
filtros óptimos para ruidos aditivos y substractivos, respectivamente.
Ruido aditivo:
Imagen con ruido: S 
N
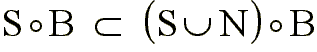
Por ser antiextensivo cumple que:
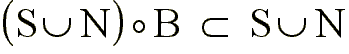
con lo que se puede expresar
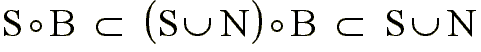
Si es posible elegir uno o varios B que cumplan ser invariantes
para S, es decir, que 
,
se tendrá que:
esto es, que la imagen con ruido filtrada siempre se aproximará
a la imagen inicial.
Filtros secuenciales alternativos.
Son combinaciones secuenciales de distintos tipos de filtros,
tales como: