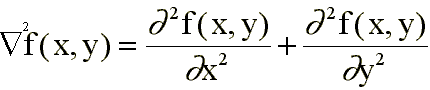
Se define el operador Laplaciana de un función f(x,y) como
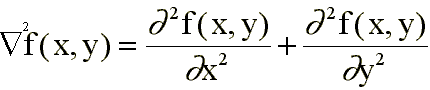
Es corriente emplear discretizaciones aproximadas tales como
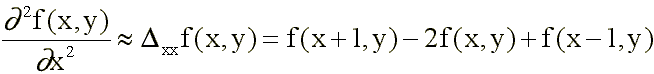
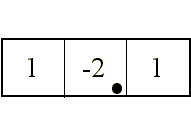
no siendo necesario, en este caso, desplazar los bordes, pues se realizan dos desplazamientos opuestos de valor 0.5 píxels
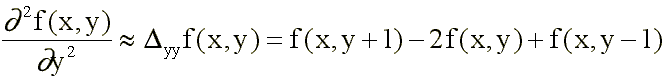
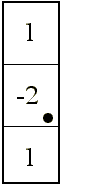
La acción conjunta de estas dos máscaras sería:
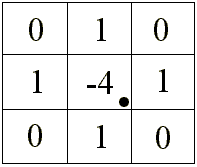
Este operador es isotrópico
y lineal y su aplicación a la imagen inicial de prácticas
puede verse en el siguiente ejemplo:
 |
 |
|
|
|
|
|
donde se aprecia la doble transición que genera un borde y que se corresponde con el valor absoluto de la segunda derivada (existe un paso por cero).
Si se considera la laplaciana en cuatro ejes separados 45º (X-Y-R-C), tendremos:
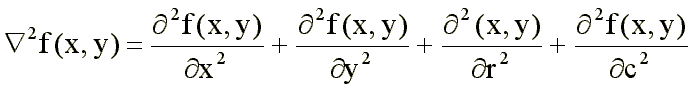
y la máscara correspondiente sería:
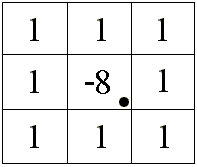
Su aplicación a la imagen inicial
de prácticas puede verse en el siguiente ejemplo:
 |
 |
|
|
|
|
|
donde se aprecia la doble transición que genera un borde y que se corresponde con el valor absoluto de la segunda derivada (existe un paso por cero).