Se define la derivada de la función f(x,y) en la dirección a (ángulo formado con el eje X), con vector unitario , como:

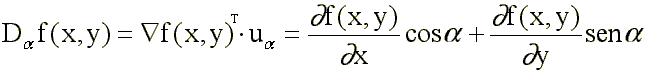
    Si se selecciona como dirección la del gradiente (q), se puede definir la derivada en la dirección del gradiente como:

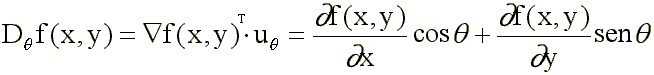
    Si se escoge como vector el propio gradiente

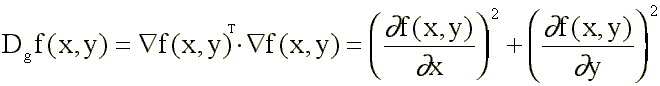
    Un ejemplo de esto puede observarse comparando las dos imágenes siguientes:
 

Imagen inicial.		Primera derivada direccional.

    La importancia de este operador es que es isotrópico (hay independencia entre la dirección del borde y de los ejes). Por contra, no es lineal.