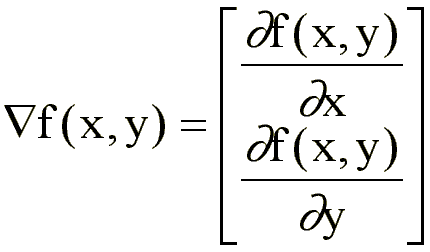
Se define el vector gradiente de una función f(x,y) como:
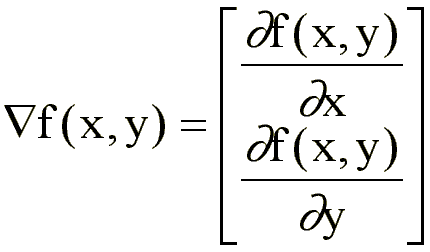
Ligados al gradiente se definen también:
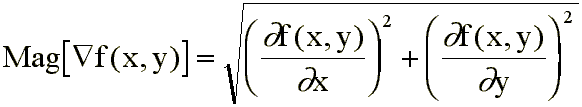
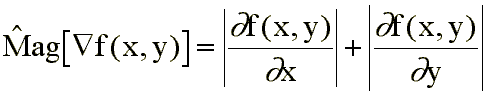
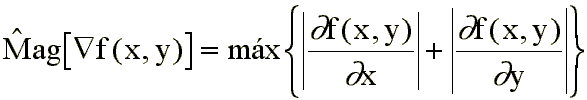
 |
 |
|
|
|
|
|
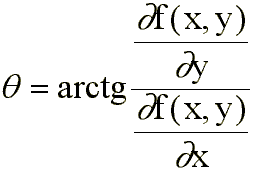
donde q representa el ángulo con el eje X.El vector unitario en la dirección del gradiente será:Por ejemplo, para una pieza rectangular con los ejes X-Y, y definiendo el gradiente como la transición oscuro-claro, el ángulo del gradiente tomará los valores representados en la siguiente figura para los puntos del borde.
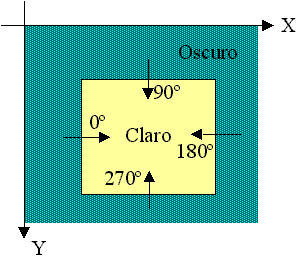
Valores de inclinación del gradiente en función de los ejes.
En las siguientes imágenes se aprecian los valores que toma el ángulo del gradiente escalado entre 0 y 255 (en vez de entre 0º y 360º).
Imagen "INICIAL" de prácticas. Argumento del gradiente para la imagen anterior.
Los bordes comprendidos entre 110 y 130 (155.3º y 183.5 º) serán los representados en la siguiente figura.

Puntos cuyo argumento del
gradiente se encuentra
comprendido entre 110 y 130.

Es corriente emplear discretizaciones aproximadas tales como:
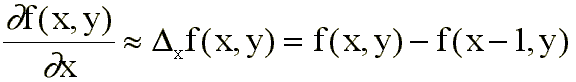

donde el punto • indica el elemento central.
La convolución con esta máscara
ocasiona el desplazamiento de los bordes en una cantidad positiva de 0.5
píxels. La convolución de una imagen con esta máscara
se observa en las siguientes imágenes:
 |
 |
|
|
|
|
|
Si se utiliza la aproximación
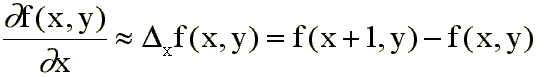
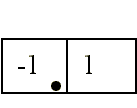
se producirá un desplazamiento negativo en los bordes de valor -0.5 píxels. Para el eje Y quedaría:
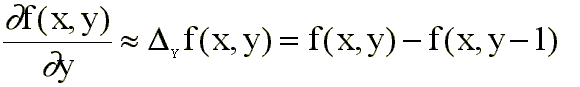
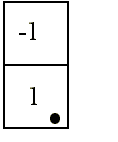
El efecto de esta convolución
se puede observar comparando las dos imágenes siguientes:
 |
 |
|
|
|
|
|
Con estas aproximaciones, y por razones
computacionales, se suele emplear la magnitud del gradiente (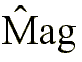 )
definida de la siguiente forma:
)
definida de la siguiente forma:
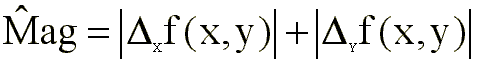
con
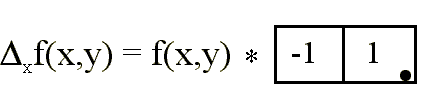
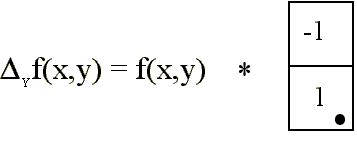
También produce buenos resultados
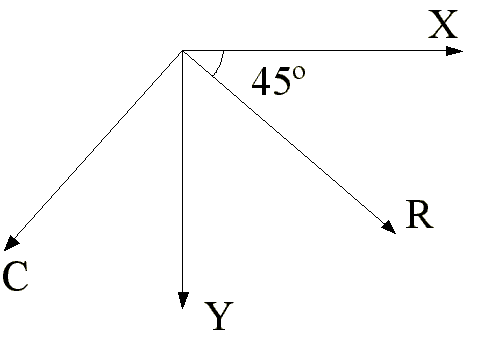
definir los incrementos sobre ejes perpendiculares (R-C) rotados 45º
sobre los tradicionales (X-Y).
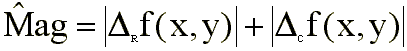
con
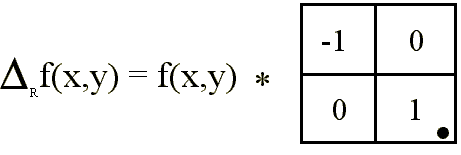
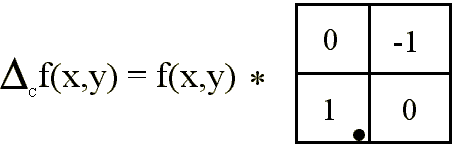
En las siguientes imágenes se
muestran los resultados de convolvucionar la imagen inicial con las dos
anteriores máscaras:

Imagen de inicial.
 |
 |
|
|
|
|
|