Approximates Freeman chain(s) with polygonal curve
CvSeq* cvApproxChains( CvSeq* srcSeq, CvMemStorage* storage,
CvChainApproxMethod method=CV_CHAIN_APPROX_SIMPLE,
double parameter=0, int minimalPerimeter=0, int recursive=0 );
This is a stand-alone approximation routine. The function cvApproxChains works exactly in the same way as cvFindContours with the corresponding approximation flag. The function returns pointer to the first resultant contour. Other approximated contours, if any, can be accessed via v_next or h_next fields of the returned structure.
Initializes chain reader
void cvStartReadChainPoints( CvChain* chain, CvChainPtReader* reader );
The function cvStartReadChainPoints initializes a special reader (see Dynamic Data Structures for more information on sets and sequences).
Gets next chain point
CvPoint cvReadChainPoint( CvChainPtReader* reader );
The function cvReadChainPoint returns the current chain point and updates the reader position.
Approximates polygonal curve(s) with desired precision
CvSeq* cvApproxPoly( const void* srcSeq, int headerSize, CvMemStorage* storage,
int method, double parameter,
int parameter2=0 );
The function cvApproxPoly approximates one or more curves and returns the approximation result[s]. In case of multiple curves approximation the resultant tree will have the same structure as the input one (1:1 correspondence).
Calculates up-right bounding rectangle of point set
CvRect cvBoundingRect( CvArr* contour, int update );
The function cvBoundingRect returns the up-right bounding rectangle for 2d point set.
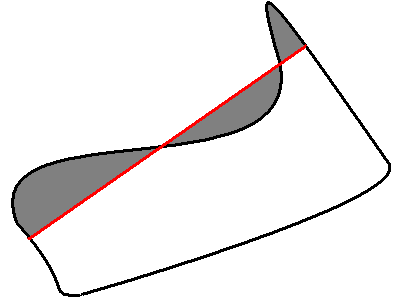
Calculates area of the whole contour or contour section
double cvContourArea( const CvArr* contour, CvSlice slice=CV_WHOLE_SEQ );
The function cvContourArea calculates area of the whole contour or contour section. In the latter case the total area bounded by the contour arc and the chord connecting the 2 selected points is calculated as shown on the picture below:

NOTE: Orientation of the contour affects the area sign, thus the function may return negative result. Use fabs() function from C runtime to get the absolute value of area.
Calculates contour perimeter or curve length
double cvArcLength( const void* curve, CvSlice slice=CV_WHOLE_SEQ, int isClosed=-1 );
The function cvArcLength calculates length or curve as sum of lengths of segments between subsequent points
Compares two shapes
double cvMatchShapes( const void* A, const void* B,
int method, double parameter=0 );
The function cvMatchShapes compares two shapes. The 3 implemented methods all use Hu moments (see cvGetHuMoments):
method=CV_CONTOUR_MATCH_I1: I1(A,B)=sumi=1..7abs(1/mAi - 1/mBi) method=CV_CONTOUR_MATCH_I2: I2(A,B)=sumi=1..7abs(mAi - mBi) method=CV_CONTOUR_MATCH_I3: I3(A,B)=sumi=1..7abs(mAi - mBi)/abs(mAi) where mAi=sign(hAi)•log(hAi), mBi=sign(hBi)•log(hBi), hAi, hBi - Hu moments of A and B, respectively.
Creates hierarchical representation of contour
CvContourTree* cvCreateContourTree( cont CvSeq* contour, CvMemStorage* storage, double threshold );
The function cvCreateContourTree creates binary tree representation for the input contour and returns the pointer to its root. If the parameter threshold is less than or equal to 0, the function creates full binary tree representation. If the threshold is greater than 0, the function creates representation with the precision threshold: if the vertices with the interceptive area of its base line are less than threshold, the tree should not be built any further. The function returns the created tree.
Restores contour from tree
CvSeq* cvContourFromContourTree( const CvContourTree* tree, CvMemStorage* storage,
CvTermCriteria criteria );
The function cvContourFromContourTree restores the contour from its binary tree representation. The parameter criteria determines the accuracy and/or the number of tree levels used for reconstruction, so it is possible to build approximated contour. The function returns reconstructed contour.
Compares two contours using their tree representations
double cvMatchContourTrees( const CvContourTree* tree1, const CvContourTree* tree2,
CvTreeMatchMethod method, double threshold );
The function cvMatchContourTrees calculates the value of the matching measure for two contour trees. The similarity measure is calculated level by level from the binary tree roots. If at the certain level difference between contours becomes less than threshold, the reconstruction process is interrupted and the current difference is returned.
Finds bounding rectangle for two given rectangles
CvRect cvMaxRect( const CvRect* rect1, const CvRect* rect2 );
The function cvMaxRect finds minimum area rectangle that contains both input rectangles inside:

Rotated 2D box
typedef struct CvBox2D
{
CvPoint2D32f center; /* center of the box */
CvSize2D32f size; /* box width and length */
float angle; /* angle between the horizontal axis
and the first side (i.e. length) in radians */
}
CvBox2D;
Finds box vertices
void cvBoxPoints( CvBox2D box, CvPoint2D32f pt[4] );
The function cvBoxPoints calculates vertices of the input 2d box. Here is the function code:
void cvBoxPoints( CvBox2D box, CvPoint2D32f pt[4] )
{
float a = (float)cos(box.angle)*0.5f;
float b = (float)sin(box.angle)*0.5f;
pt[0].x = box.center.x - a*box.size.height - b*box.size.width;
pt[0].y = box.center.y + b*box.size.height - a*box.size.width;
pt[1].x = box.center.x + a*box.size.height - b*box.size.width;
pt[1].y = box.center.y - b*box.size.height - a*box.size.width;
pt[2].x = 2*box.center.x - pt[0].x;
pt[2].y = 2*box.center.y - pt[0].y;
pt[3].x = 2*box.center.x - pt[1].x;
pt[3].y = 2*box.center.y - pt[1].y;
}
Fits ellipse to set of 2D points
CvBox2D cvFitEllipse2( const CvArr* points );
The function cvFitEllipse calculates ellipse that fits best (in least-squares sense) to a set of 2D points. The meaning of the returned structure fields is similar to those in cvEllipse except that size stores the full lengths of the ellipse axises, not half-lengths
Fits line to 2D or 3D point set
void cvFitLine( const CvArr* points, CvDisType disType, double C,
double reps, double aeps, float* line );
The function cvFitLine fits line to 2D or 3D point set by minimizing sumiρ(ri), where ri is distance between i-th point and the line and ρ(r) is a distance function, one of:
disType=CV_DIST_L2 (L2):
ρ(r)=r2/2 (the simplest and the fastest least-squares method)
disType=CV_DIST_L1 (L1):
ρ(r)=r
disType=CV_DIST_L12 (L1-L2):
ρ(r)=2•[sqrt(1+r2/2) - 1]
disType=CV_DIST_FAIR (Fair):
ρ(r)=C2•[r/C - log(1 + r/C)], C=1.3998
disType=CV_DIST_WELSCH (Welsch):
ρ(r)=C2/2•[1 - exp(-(r/C)2)], C=2.9846
disType=CV_DIST_HUBER (Huber):
ρ(r)= r2/2, if r < C
C•(r-C/2), otherwise; C=1.345
Finds convex hull of points set
CvSeq* cvConvexHull2( const void* points, void* hullStorage=0,
int orientation=CV_CLOCKWISE, int returnPoints=0 );
The function cvConvexHull2 finds convex hull of 2D point set using Sklansky's algorithm. If hullStorage is memory storage, the function creates a sequence containing the hull points or pointers to them, depending on returnPoints value and returns the sequence on output.
#include "cv.h"
#include "highgui.h"
#include <stdlib.h>
#define ARRAY 0 /* switch between array/sequence method by replacing 0<=>1 */
void main( int argc, char** argv )
{
IplImage* img = cvCreateImage( cvSize( 500, 500 ), 8, 3 );
cvNamedWindow( "hull", 1 );
#if !ARRAY
CvMemStorage* storage = cvCreateMemStorage();
#endif
for(;;)
{
int i, count = rand()%100 + 1, hullcount;
CvPoint pt0;
#if !ARRAY
CvSeq* ptseq = cvCreateSeq( CV_SEQ_KIND_GENERIC|CV_32SC2, sizeof(CvContour),
sizeof(CvPoint), storage );
CvSeq* hull;
for( i = 0; i < count; i++ )
{
pt0.x = rand() % (img->width/2) + img->width/4;
pt0.y = rand() % (img->height/2) + img->height/4;
cvSeqPush( ptseq, &pt0 );
}
hull = cvConvexHull2( ptseq, 0, CV_CLOCKWISE, 0 );
hullcount = hull->total;
#else
CvPoint* points = (CvPoint*)malloc( count * sizeof(points[0]));
int* hull = (int*)malloc( count * sizeof(hull[0]));
CvMat pointMat = cvMat( 1, count, CV_32SC2, points );
CvMat hullMat = cvMat( 1, count, CV_32SC1, hull );
for( i = 0; i < count; i++ )
{
pt0.x = rand() % (img->width/2) + img->width/4;
pt0.y = rand() % (img->height/2) + img->height/4;
points[i] = pt0;
}
cvConvexHull2( &pointMat, &hullMat, CV_CLOCKWISE, 0 );
hullcount = hullMat.cols;
#endif
cvZero( img );
for( i = 0; i < count; i++ )
{
#if !ARRAY
pt0 = *CV_GET_SEQ_ELEM( CvPoint, ptseq, i );
#else
pt0 = points[i];
#endif
cvCircle( img, pt0, 2, CV_RGB( 255, 0, 0 ), CV_FILLED );
}
#if !ARRAY
pt0 = **CV_GET_SEQ_ELEM( CvPoint*, hull, hullcount - 1 );
#else
pt0 = points[hull[hullcount-1]];
#endif
for( i = 0; i < hullcount; i++ )
{
#if !ARRAY
CvPoint pt = **CV_GET_SEQ_ELEM( CvPoint*, hull, i );
#else
CvPoint pt = points[hull[i]];
#endif
cvLine( img, pt0, pt, CV_RGB( 0, 255, 0 ));
pt0 = pt;
}
cvShowImage( "hull", img );
int key = cvWaitKey(0);
if( key == 27 ) // 'ESC'
break;
#if !ARRAY
cvClearMemStorage( storage );
#else
free( points );
free( hull );
#endif
}
}
Tests contour convex
int cvCheckContourConvexity( const void* contour );
The function cvCheckContourConvexity tests whether the input contour is convex or not. The contour must be simple, i.e. without self-intersections.
Structure describing a single contour convexity detect
typedef struct CvConvexityDefect
{
CvPoint* start; /* point of the contour where the defect begins */
CvPoint* end; /* point of the contour where the defect ends */
CvPoint* depth_point; /* the farthest from the convex hull point within the defect */
float depth; /* distance between the farthest point and the convex hull */
} CvConvexityDefect;

Finds convexity defects of contour
CvSeq* cvConvexityDefects( const void* contour, const void* convexhull,
CvMemStorage* storage=0 );
The function cvConvexityDefects finds all convexity defects of the input contour and returns a sequence of the CvConvexityDefect structures.
Finds circumscribed rectangle of minimal area for given 2D point set
CvBox2D cvMinAreaRect2( const void* points, CvMemStorage* storage=0 );
The function cvMinAreaRect2 finds a circumscribed rectangle of the minimal area for 2D point set by building convex hull for the set and applying rotating calipers technique to the hull.
Finds circumscribed circle of minimal area for given 2D point set
void cvMinEnclosingCircle( const void* points, CvPoint2D32f* center, float* radius );
The function cvMinEnclosingCircle finds the minimal circumscribed circle for 2D point set using iterative algorithm.
Calculates pair-wise geometrical histogram for contour
void cvCalcPGH( const CvSeq* contour, CvHistogram* hist );
The function cvCalcPGH calculates 2D pair-wise geometrical histogram (PGH), described in [Iivarinen97], for the contour. The algorithm considers every pair of the contour edges. The angle between the edges and the minimum/maximum distances are determined for every pair. To do this each of the edges in turn is taken as the base, while the function loops through all the other edges. When the base edge and any other edge are considered, the minimum and maximum distances from the points on the non-base edge and line of the base edge are selected. The angle between the edges defines the row of the histogram in which all the bins that correspond to the distance between the calculated minimum and maximum distances are incremented (that is, the histogram is transposed relatively to [Iivarninen97] definition). The histogram can be used for contour matching.
[Iivarinen97] Jukka Iivarinen, Markus Peura, Jaakko Srel, and Ari Visa. Comparison of Combined Shape Descriptors for Irregular Objects, 8th British Machine Vision Conference, BMVC'97. You may find online version at http://www.cis.hut.fi/research/IA/paper/publications/bmvc97/bmvc97.html
Splits set of vectors by given number of clusters
void cvKMeans2( const CvArr* samples, int numClusters,
CvArr* clusterIdx, CvTermCriteria termcrit );
The function cvKMeans2 implements k-means algorithm that finds centers of numClusters clusters and groups the input samples around the clusters. On output clusterIdx(i) contains a cluster index for sample stored in i-th rows of samples.
#include "cv.h"
#include "highgui.h"
void main( int argc, char** argv )
{
#define MAX_CLUSTERS 5
static const int color_tab[MAX_CLUSTERS] =
{
CV_RGB(255,0,0), CV_RGB(0,255,0), CV_RGB(100,100,255),
CV_RGB(255,0,255), CV_RGB(255,255,0)
};
IplImage* img = cvCreateImage( cvSize( 500, 500 ), 8, 3 );
CvRandState rng;
cvRandInit( &rng, 0, 1, -1, CV_RAND_NORMAL );
cvNamedWindow( "clusters", 1 );
for(;;)
{
int k, cluster_count = cvRandNext(&rng)%MAX_CLUSTERS + 1;
int i, sample_count = cvRandNext(&rng)%1000 + 1;
CvMat* points = cvCreateMat( sample_count, 1, CV_32FC2 );
CvMat* clusters = cvCreateMat( sample_count, 1, CV_32SC1 );
/* generate random sample from multigaussian distribution */
for( k = 0; k < cluster_count; k++ )
{
CvPoint center;
CvMat point_chunk;
center.x = cvRandNext(&rng)%img->width;
center.y = cvRandNext(&rng)%img->height;
cvRandSetRange( &rng, center.x, img->width/6, 0 );
cvRandSetRange( &rng, center.y, img->height/6, 1 );
cvGetRows( points, &point_chunk, k*sample_count/cluster_count,
k == cluster_count - 1 ? sample_count : (k+1)*sample_count/cluster_count );
cvRand( &rng, &point_chunk );
}
/* shuffle samples */
for( i = 0; i < sample_count/2; i++ )
{
CvPoint2D32f* pt1 = (CvPoint2D32f*)points->data.fl + cvRandNext(&rng)%sample_count;
CvPoint2D32f* pt2 = (CvPoint2D32f*)points->data.fl + cvRandNext(&rng)%sample_count;
CvPoint2D32f temp;
CV_SWAP( *pt1, *pt2, temp );
}
cvKMeans2( points, cluster_count, clusters,
cvTermCriteria( CV_TERMCRIT_EPS+CV_TERMCRIT_ITER, 10, 1.0 ));
cvZero( img );
for( i = 0; i < sample_count; i++ )
{
CvPoint2D32f pt = ((CvPoint2D32f*)points->data.fl)[i];
int cluster_idx = clusters->data.i[i];
cvCircle( img, cvPointFrom32f(pt), 2, color_tab[cluster_idx], CV_FILLED );
}
cvReleaseMat( &points );
cvReleaseMat( &clusters );
cvShowImage( "clusters", img );
int key = cvWaitKey(0);
if( key == 27 ) // 'ESC'
break;
}
}
Finds circumscribed circle of minimal area for given 2D point set
void cvMinEnclosingCircle( const void* points, CvPoint2D32f* center, float* radius );
The function cvMinEnclosingCircle finds the minimal circumscribed circle for 2D point set using iterative algorithm.
Planar subdivision
#define CV_SUBDIV2D_FIELDS() \
CV_GRAPH_FIELDS() \
int quad_edges; \
int is_geometry_valid; \
CvSubdiv2DEdge recent_edge; \
CvPoint2D32f topleft; \
CvPoint2D32f bottomright;
typedef struct CvSubdiv2D
{
CV_SUBDIV2D_FIELDS()
}
CvSubdiv2D;
Planar subdivision is a subdivision of a plane into a set of non-overlapped regions (facets) that cover the whole plane. The above structure describes a subdivision built on 2d point set, where the points are linked together and form a planar graph, which, together with a few edges connecting exterior subdivision points (namely, convex hull points) with infinity, subdivides a plane into facets by its edges.
For every subdivision there exists dual subdivision there facets and points (subdivision vertices) swap their roles, that is, a facet is treated as a vertex (called virtual point below) of dual subdivision and the original subdivision vertices become facets. On the picture below original subdivision is marked with solid lines and dual subdivision with dot lines

OpenCV subdivides plane into triangles using Delaunay's algorithm. Subdivision is built iteratively starting from a dummy triangle that includes all the subdivision points for sure. In this case the dual subdivision is Voronoi diagram of input 2d point set. The subdivisions can be used for 3d piece-wise transformation of a plane, morphing, fast location of points on the plane, building special graphs (such as NNG,RNG) etc.
Quad-edge of planar subdivision
/* one of edges within quad-edge, lower 2 bits is index (0..3)
and upper bits are quad-edge pointer */
typedef long CvSubdiv2DEdge;
/* quad-edge structure fields */
#define CV_QUADEDGE2D_FIELDS() \
int flags; \
struct CvSubdiv2DPoint* pt[4]; \
CvSubdiv2DEdge next[4];
typedef struct CvQuadEdge2D
{
CV_QUADEDGE2D_FIELDS()
}
CvQuadEdge2D;
Quad-edge is a basic element of subdivision, it contains four edges (e, eRot and reversed e & eRot):

Point of original or dual subdivision
#define CV_SUBDIV2D_POINT_FIELDS()\
int flags; \
CvSubdiv2DEdge first; \
CvPoint2D32f pt;
#define CV_SUBDIV2D_VIRTUAL_POINT_FLAG (1 << 30)
typedef struct CvSubdiv2DPoint
{
CV_SUBDIV2D_POINT_FIELDS()
}
CvSubdiv2DPoint;
Returns one of edges related to given
CvSubdiv2DEdge cvSubdiv2DGetEdge( CvSubdiv2DEdge edge, CvNextEdgeType type ); #define cvSubdiv2DNextEdge( edge ) cvSubdiv2DGetEdge( edge, CV_NEXT_AROUND_ORG )
The function cvSubdiv2DGetEdge returns one the edges related to the input edge.
Returns another edge of the same quad-edge
CvSubdiv2DEdge cvSubdiv2DRotateEdge( CvSubdiv2DEdge edge, int rotate );
The function cvSubdiv2DRotateEdge returns one the edges of the same quad-edge as the input edge.
Returns edge origin
CvSubdiv2DPoint* cvSubdiv2DEdgeOrg( CvSubdiv2DEdge edge );
The function cvSubdiv2DEdgeOrg returns the edge origin. The returned pointer may be NULL if the edge is from dual subdivision and the virtual point coordinates are not calculated yet. The virtual points can be calculated using function cvCalcSubdivVoronoi2D.
Returns edge destination
CvSubdiv2DPoint* cvSubdiv2DEdgeDst( CvSubdiv2DEdge edge );
The function cvSubdiv2DEdgeDst returns the edge destination. The returned pointer may be NULL if the edge is from dual subdivision and the virtual point coordinates are not calculated yet. The virtual points can be calculated using function cvCalcSubdivVoronoi2D.
Creates empty Delaunay triangulation
CvSubdiv2D* cvCreateSubdivDelaunay2D( CvRect rect, CvMemStorage* storage );
The function cvCreateSubdivDelaunay2D creates an empty Delaunay subdivision, where 2d points can be added further using function cvSubdivDelaunay2DInsert. All the points to be added must be within the specified rectangle, otherwise a runtime error will be raised.
Inserts a single point to Delaunay triangulation
CvSubdiv2DPoint* cvSubdivDelaunay2DInsert( CvSubdiv2D* subdiv, CvPoint2D32f pt);
The function cvSubdivDelaunay2DInsert inserts a single point to subdivision and modifies the subdivision topology appropriately. If a points with same coordinates exists already, no new points is added. The function returns pointer to the allocated point. No virtual points coordinates is calculated at this stage.
Inserts a single point to Delaunay triangulation
CvSubdiv2DPointLocation cvSubdiv2DLocate( CvSubdiv2D* subdiv, CvPoint2D32f pt,
CvSubdiv2DEdge *edge,
CvSubdiv2DPoint** vertex=0 );
The function cvSubdiv2DLocate locates input point within subdivision. There are 5 cases:
Finds the closest subdivision vertex to given point
CvSubdiv2DPoint* cvFindNearestPoint2D( CvSubdiv2D* subdiv, CvPoint2D32f pt );
The function cvFindNearestPoint2D is another function that locates input point within subdivision. It finds subdivision vertex that is the closest to the input point. It is not necessarily one of vertices of the facet containing the input point, though the facet (located using cvSubdiv2DLocate) is used as a starting point. The function returns pointer to the found subdivision vertex
Calculates coordinates of Voronoi diagram cells
void cvCalcSubdivVoronoi2D( CvSubdiv2D* subdiv );
The function cvCalcSubdivVoronoi2D calculates coordinates of virtual points. All virtual points corresponding to some vertex of original subdivision form (when connected together) a boundary of Voronoi cell of that point.
Removes all virtual points
void cvClearSubdivVoronoi2D( CvSubdiv2D* subdiv );
The function cvClearSubdivVoronoi2D removes all virtual points. It is called internally in cvCalcSubdivVoronoi2D if the subdivision was modified after previous call to the function.
There are a few other lower-level functions that work with planar subdivisions, see cv.h and the sources. Demo script delaunay.c that builds Delaunay triangulation and Voronoi diagram of random 2d point set can be found at opencv/samples/c.