Rather than describing each screen and menu in SOLVESYS 49, I'll provide some examples instead.
Basic usage is described in the first example so please start from here even though you may not be interested in solving linear equations.
Example 1: Solving a system of linear equations
Although the HP49G already has built-in functions to solve systems of linear equations (such as LINSOLVE), you may find it convenient to use SOLVESYS instead. At least this small example should give you an idea of how to use SOLVESYS.
The system we want to solve is:
-
2x + y = 3x + z
-
z + x = 2(x + y)
- (z + x)/2 + y + 1.2 = 0
There are several ways to start SOLVESYS. The fastest way is open the NUM.SLV choose menu and select SOLVESYS 1.2 from here.
The first thing SOLVESYS displays, is a list of equations to be solved. This is actually the contents of the 'EQ' variable so if there's no 'EQ' variable in the current directory an empty list is displayed. For example, if the above equations are stored as a list in 'EQ' prior to starting SOLVESYS, the opening display should look something like this:

If you haven't stored the equations in 'EQ', use [ADD] to enter the equations.
The checkmark indicates that the equation is marked for solving (default). If there are equations you don't want to solve, use the [+/-] key to uncheck them - this has the same effect as [DEL] but does not remove the equation from 'EQ'.
Now press [OK] to proceed. SOLVESYS analyzes the equations for variables and opens the "Variables" screen shown below.

You can modify a highlighted value using the [EDIT] menukey or [ENTER]. To check/uncheck a variable, use the [+/-] key. The [RESET] key sets all variables equal to 1.
- Checked variables will be solved for (default). A real or complex valued starting guess must be provided. This should be your best guess of the solution you're looking for - don't use the default values if you know any better.
- Unchecked variables are not solved for and the value remain constant during the solving process. In fact, the value need not be a real or complex numbers, however the equations must eventually evaluate to a number.
In this example, we want to solve for all variables so all must be checked. The starting values are unimportant because the equations are linear. If we use the default values as shown and press [SOLVE] we get the next screens:


Here "Zero" indicates that a solution has been found. When returned to the "Variables" screen, the final values are displayed.
As you can see, the solution is (x, y, z) = (0.4, -0.8, -1.2). When you exit SOLVESYS, these values will be stored in their respective variables. However you can also use [->STK] to copy this solution (as well as a error vector) to the stack
Example 2: Solving a system of nonlinear equations.
In this example we will solve a rather large system (propane combustion?) which is a mixture of 11 linear and nonlinear equations in 11 unknowns (x1,...,x11) and seven known variables (a1,...,a6 and r).
| x1 + x4 = 3 2x1 + x2 + x4 + x7 + x8 + x9 + 2x10 = 10 + r x2 + 2x5 + x6 + x7 = 8 2x3 + x5 = 4r x1 x5 = a1 x2 x4 x6 x2½ = a2 (x2 x4 x11)½ x7 x4½ = a3 (x1 x4 x11)½ x8 x4 = a4 x2 x11 x9 x4 = a5 x1 (x3 x11)½ x10 x42 = a6 x42 x11 x11 = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 |
a1 = 0.193 a2 = 0.002597 a3 = 0.003448 a4 = 0.00001799 a5 = 0.0002155 a6 = 0.00003846 r = 4.056734 |
In SOLVESYS, this equation set will look like:
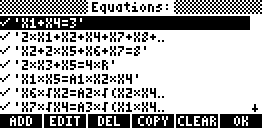
All the equations should be included (checked). Press [OK] to open the "Variables" screen:

Remember that the first seven values here are constants. These must be unchecked and filled in with their corresponding values shown earlier. For the unknowns we will use 1 as the initial value except x11 we set to 10 since x11 is the sum of the other variables (equation 11).
When finished, the display should then look something like the one below. Use the downarrow key to view/edit the remaining variables.
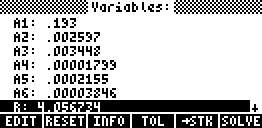

[Note: To verify that you have the correct amount of unknowns, press [INFO] menukey. This should show "m/n = 11/11" which means that 11 equations and 11 variables are selected to be solved]
When done, press [SOLVE]and after a few minutes a solution (Zero) is found:

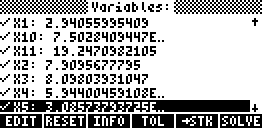
The final values can be viewed using the up/downarrow keys. [->STK] can be used to copy the result and the equation residuals the stack (do this!). Note that the values are also stored in the variables after you exit SOLVESYS.
Example 3: Nonlinear least-squares
If there are more (generally inconsistent) equations than unknowns, SOLVESYS will search for a "best fit" solution in the least-squares sense, ie. a solution that minimizes the sum of squared equations deviations.
A common application of least-squares minimization is datafitting, where one is attempting to fit m observations to an expression of n unknown parameters for which the "best-fit" values are required. If each observation is inserted in the expression, the result is a system of m "observational" equations in n unknowns.
Here's an example.
The relationship between the measured pressure and temperature in saturated steam can be written as
Y=a*ALOG(b*T/(c+T))
where Y is the measured pressure of the steam at various values of a
controllable temperature T
a, b and c are unknown parameters (to be estimated)
The following data were collected.
| T | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 85 | 90 | 95 | 100 | 105 |
| Y | 4.14 | 8.52 | 16.31 | 32.18 | 64.62 | 98.76 | 151.13 | 224.74 | 341.35 | 423.36 | 522.78 | 674.32 | 782.04 | 920.01 |
To create the 14 equations needed, perform the following four steps:
- Store the data as lists in variables such as 'T' and 'Y'.
- If any of the variables A, B or C exist, they must be purged.
- Enter 'Y=A*ALOG(B*T/(C ADD T))'on the stack and press [EVAL]
- You're done! Store the resulting list of equations in the 'EQ' variable.
[IMPORTANT: In step 3. you must replace any occurence of "+" with "ADD" or "--" since "+" has a different action when list are involved.]
As for the initial guesses, note that the first equation is actually A=4.14 so this can be used as a guess. If A=4.14 is inserted in the next two equations, these can be reduced to two linear equations with the solution (b,c) = (5.93,179). Thus an initial guess could be (a,b,c)=(4,6,180).
Now we're ready to start SOLVESYS. The equations are already created so press [OK] and fill in the guess values (a,b,c) = (4, 6, 180)
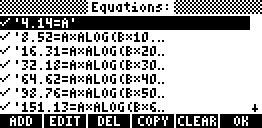

Press [SOLVE] and answer "yes" to accept that m is different from n (since we have more equations than unknowns). After a few iterations a solution (minimum) is found.



Using 3 significant digits, the best fit function is Y(T)=5.27*ALOG[8.56*T/(295+T)].
Be aware that there are no simple ways to distinguish between a local or global minimum so the choice of starting values is very crucial. A good initial guess is not only a real time-saver, it will also pick out the right (global) minimum for you!